Electric charges and fields :- Notes

Notes :-

Hey Guys!!

Here i am providing you notes of chapter 1 class 12th physics.. These are notes of what I taught in youtube videos.. so that you can revise your concepts accordingly… These are the notes of Electric charges and fields (from Electrostatics)..

Hope this may help you… 😊

Electrostatic- charges at rest. {study of charges when charges are static(at rest) }.

Electric Charges - Intrinsic property of a matter.

Origin - Around 600BC -Thales of melatus, Greece

Types of charges- To distinguish different charges Benjamin Franklin gave polarity - positive charge and negative charge.

How is a charge created??? By friction (Rubbing) -

When two objects rubbed together they generate energy and loosely bounded electrons are removed.

Object from which electrons are removed .. becomes positively charged.

Object which gains electrons becomes negatively charged

Equal number of protons and electrons- object is said to be neutral. Otherwise called Electrified or Charged when number of electrons and protons are not equal in an atom.

Some examples of friction -

Glass rod with silk cloth

Plastic rod with fur

Ebonite rod with silk

By conduction- (By touching)

Take one charged metal sphere( positively charge) and one uncharged sphere ... keep both in contact with each other .. similar charge is created on uncharged sphere.

As metals are conductors they allow the charges to flow.. Hence electrons from uncharged sphere move towards charged sphere and +ve charge is created...

By induction-

Take one uncharged sphere ... one charged( +vely charged) rod...place charged rod near uncharged sphere( don’t touch it with sphere) ... The near end will acquire charge of opposite polarity and farther end acquires charge of similar polarity as the rod.

Q What are the properties of charges

A 1) Charges are additive in nature .

2) Charges are Conserved.

3) Quantisation of charge.

4) Invariance of charge.

5) Like charges repel while unlike charges attract each other.

Properties of charges :-

i) Additive Nature of Charge-

The total electric charge on an object is equal to the algebraic sum of all the electric charge distributed on different parts of the object.

As we do algebraic sum of masses to calculate total mass .. similarly we do algebraic sum of charges to get total charge.. Both are scalar quantities. But there are some differences between the two also -

CHARGE	MASS
1) Electric charge can be positive ,negative or zero.	Mass of body is always positive.
2) Charge can be quantized , q=ne.	Quantization is yet to be proved.
3) Electric charge is always conserved.	Mass is not conserved as it can be changed into energy and vice versa.
4) Forces between charges can be attractive or repulsive depending whether they are unlike or like.	The gravitational force between two masses is always attractive.
5) Charge present on a body does not depend on the velocity of the body.	Mass of a body increases with its velocity according to the relativistic mass variation formula- -> m = m0/√1-v²/c²
6) A charged body always possesses some mass.	A body possessing mass may not have any net charge.
7) Electrostatic forces between different charges may cancel out.	Gravitational forces between different masses never cancel out.

ii) Quantization of Electric charge-

Least charge found on bodies is equal to one electron’s or one proton’s. The quantization of electric charge is the property by virtue of which any charge can exists only in discrete lumps or packets of certain minimum charge e. The cause of quantization is that only integral no. of electrons can be transferred from one body to another.

The charge on an object can be increased or decreased in steps of e. It is known as quantization of charge.

Mathematically, Q = ± ne

Where n is integer and e is basic or fundamental charge ..

e = 1.6 x 10^-19 C

iii) Conservation of Charge -

According to principle of conservation of charge, net charge in any isolated system always remains constant.

In any physical process, charge may get transferred from one body to the other but net charge remains same. Charge can neither be created nor can be destroyed.

Examples:- 1) Transfer of charge from glass rod to silk. The system of glass rod and silk, which had zero net charge before and after rubbing.

2) Pair Production and pair annihilation. Pair Production- When gamma rays strikes the nucleus, then a pair of electron and positron is formed. Gamma rays being photon have zero charge and net charge on electron and position is also zero. Pair Annihilation- When an electron and positron come near to each other, they eliminate a gamma ray , hence total charge becomes zero.

Coulomb's Law or Electrostatic force :-

The electrostatic forces or Coulomb force is the force of attraction or repulsion between two static point charges.

Like gravitational force it follows inverse square law.

Electrostatic force is directly proportional to the product of two charges while inversely proportional to the square of the distance between them..

Let here be 2 point charges q1 and q2 at distance r from each other at rest ( both being +ve hence repel each other)

•q1—————r—————•q2

Coulomb’s experimental observations were:-

Force of attraction or repulsion between two charges is

i) directly proportional to the magnitude of the two charges

And ii) inversely proportional to the square of the distance between them.

Mathematically,

F ∝ q1 x q2 , F ∝ 1/ r²

F = K .q1. q2 / r²

Vector form of Coulomb's law :-

Take minus sign common from F21,

Then we will get F12 = - F21

• Importance of coulomb law in vector form:-

1)It shows the force exerted by two charges are equal in magnitude and opposite in direction.

2) It also shows the electrostatic force between two charges is central force i.e, it acts along the line joining the two charges.

Importance and limitation of Coulomb’s law :-

Importance- i) It is true for point charges.

ii) True for charges at rest. For the charges in motion, other laws are given.

iii) Coulombian forced act over an enormous range of separation from nuclear dimensions (10^-15m) to macroscopic distance as large as 10^18m.

iv) It is obtained from experiments, it is experimental law.

Limitations-i) Coulombs law is not valid for extended charges.

ii)This law is not valid for a charge in motion.

iii) Not valid for r< 10^-15m .

Electrostatic force V/s Gravitational force :-

The Electrostatic force acting between two charged particles is very much greater than the gravitational force acting between them.

Eg. The electrical force between two protons is 10 to the power 36 times more greater than the gravitational forces.

Similarities:- i) Both obey inverse square law of forces. ii) both the forces operate in vacuum. iii) both the forces are conservative in nature. iv) both are central forces.

Dissimilarities :- i) Gravitational force is always attractive whereas electrostatic force can be either attractive or repulsive. ii) If an insulator is present between two charges then electrostatic force decreases whereas the medium has no effect on gravitational force. iii) Gravitational force is weak whereas electrostatic forces a strong.

Absolute and Relative permittivity :-

Medium permits its own field to decrease the interaction between the charges.

The force between two charges in air is F0 = k q1q2/ r² …(i) Where, k = 1/4πε0 Here ε0 is called absolute permittivity of air/free space and ε0 = 8.85 x 10^-12 C²/Nm² .

Now if these two charges are kept in water the force will be Fm = 1/4πεw q1 q2/ r² ……(2) and here εw = 7.12 x 10^-10 C²/ N m². Similarly, absolute permittivity of glass is εg = 3.10 x 10^-11 C²/ N m².

• ε0 < εw or εm Where εm is absolute permittivity of any medium.

These all values will be difficult for us to remember.. So we use relative permittivity…

Relative permittivity- It is defined as the ratio of permittivity of medium to permittivity of free space . Denoted by ε or εr.

i.e., ε = εm / ε0 .

On dividing i) and ii) equations we get, F0/ Fw = εw/ ε0 or εm/ ε0 = ε

Force due to multiple charges - superposition principle

The principle of superposition states that when a number of charges are interacting, the total force on a given charge is the vector sum of the individual forces exerted by the other charges on that given charge.

*The force between two charge is not affected by the presence of other charges.

Electric field:- It is a region or space around a charge.

Electric field strength- magnitude or intensity of field experienced by a small positive test charge.

The electric field intensity or the strength of the electric field at a point due to a source charge is defined as the electrostatic force per unit positive charge acting on a small test charge placed at a point without disturbing the source charge.

Consider a positive test charge q0 experiencing a force F, so the electric field is given as,

E = F / q0

But here the test charge should be so small that it should not disturb the source charge hence the expression now becomes,

E = lim F / q0 q0–>0

As force is a vector quantity and charge q0 is scalar quantity, hence the intensity of electric field E must be a vector quantity, and its direction is same as that of force F

• If test charge is positive, electric field and force will have same direction. But if test charge is negative , then the direction of field will be opposite to the force acting on negative charge.

Unit of electric field- E = F/q0 …. hence , SI unit is N/C . Dimensional formula will be [ MLT^-3A^-1]

Intensity of Electric field due to a point charge:-

Electric field due to multiple charges:-

Net electric field at a point due to number of charges will be determined using superposition principle.. which states that net electric field at a point due to other charges is the vector sum of the fields due to each charge..

Physical significance of Electric field:-

Electric field is an elegant way of characterising the electrical involvement of a system of charges.

Electric field at a point in the space around a system of charges tells us the force a unit positive test charge would experience if placed at that point.

The two physical significance of the concept of electric field emerges only when we go beyond electrostatics and deal with time-dependent electromagnetic phenomena.

Electric field lines:-

Electric field line is a way of pictorially mapping the electric field around a configuration of charges.

It is also defined as the “imaginary lines ”along which a free positive test charge would move if allowed to do so.

Properties of electric field lines:-

1) They originate from positive charge and terminate at negative charge. They do not terminate in free space.

2) They do not form closed loop.

3) Relative number of field lines is directly proportional to the magnitude of the charge.

4) Electric field lines are symmetric about the line joining the two charges.

5) The relative closeness of electric field lines is directly proportional to the magnitude of the field.

6) The tangent drawn on field line at any point gives the direction of net electric field at that point.

7) Two field lines can never intersect each other, because if they do so then at a point of intersection there will be two direction of electric field which is not possible.

8) Electric field lines are repelled by positive charge and attracted by negative charge.

9) In a uniform electric field the field lines are straight parallel and equidistant from each other.

10) Electric field lines are always perpendicular to the surface of the conductor.

Representation of electric field lines due to some charge configurations:-

Electric dipole:-

An electric dipole is a system of two equal and opposite point charges separated by a very small and finite distance.

Electric dipole moment (p) :-

An electric dipole moment is defined as the product of one of the charge and separation between the two charges.

p = q x 2l

• Electric dipole moment is a vector quantity with the direction from negative charge to positive charge . SI unit is Cm.

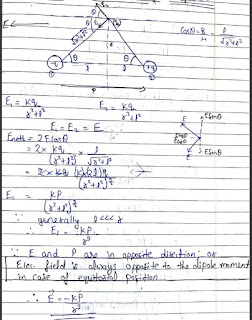
Electric field intensity on the axis of dipole :- At a distance are from the centre of dipole-

Electric field intensity on the equatorial line of the dipole :- At a distance r from centre of dipole ,

Electric field at some general point due to a short dipole :- At a distance are from the centre and angle theta from the dipole.

Electric dipole in uniform and non-uniform external electric field:-

In Uniform electric field -

When a permanent dipole of dipole moment P in a uniform external electric field E is kept there is a force QE on Q and a force minus QE on minus Q the net force on the dipole is zero since the electric field is uniform. However, the charges are separated so the force act a different point ( we say the line of action of the forces are different) hence it experiences a torque.

Maximum Torque-

Torque = PEsin θ

Torque will be maximum when sin theta will be maximum and sin theta is maximum at θ equals to 90° or 270°.

Sin θ = 1, at θ = 90° or 270°

So, torque = PE

If the strength of E =1 then, Torque = P

• Electric dipole moment is defined as the torque acting on a dipole placed perpendicular to a uniform electric field of unit is strength.

Minimum torque-

Torque will be minimum when sin theta is minimum and sin θ is minimum at either 0° or 180°.

Sin θ = 0 , when θ = 0° or 180°.

So torque = 0

And the dipole will be in equilibrium - stable or unstable

At 0° - torque = 0 and dipole is in stable equilibrium.

At 180°, torque = 0 and dipole is in unstable equilibrium.

• Electric field always tries to align a dipole along its own direction.

Non- Uniform external electric field-

Force and torque may or may not be zero in non- uniform external electric field.

• When P is parallel to E , the dipole has a net force in the direction of increasing field. When P is antiparallel to E the net force on the dipole is in the direction of decreasing field field. The force depends on the orientation of p with respect to E.

Continuous charge distribution-

When point charges are kept at a distance (separate from each other) , they are called as discrete charges. But when charges are spread uniformly either over the length of the conductor or surface of the conductor or volume of the conductor this type of distribution of charges is called continuous charge distribution

Types of charge distribution-

1) Linear charge distribution- If the charge is uniformly distributed over a straight line or that is along the length of a conductor then the distribution is called linear charge distribution.

Consider a conductor AB of length l on which charge distributed uniformly is q. In length dl, charge present is dq. In unit length charge present is dq/ dl .

++++++++++++++++++++

_________l_______________

Charge present per unit length is called linear charge density. Denoted by λ. Its SI unit is coulomb per metre.

λ = dq/dl or q/l

2) Surface charge distribution- If the charge is uniformly distributed over a surface then the distribution is called service charge distribution.

Consider a circular sheet or sphere having surface S, on which charge present is q on its surface. On surface area ds, charge present is dq. In unit surface area charge present is dq/ds.

Charge present per unit area is called surface charge density. Denoted by sigma (σ ). Its SI unit is coulomb per metre square.

σ = dq/ds or q/s

3) Volume charge distribution- If the charge is uniformly distributed over a volume that is into the bulk then the distribution is called volume charge distribution.

Consider a cube or a sphere having a volume V, inside which charge present is q. In volume dV charge present is dq. In unit volume charge present is dq/dV.

Charge present per unit volume is called volume charge density. Denoted by rho(ρ) . Its SI unit is coulomb per metre cube

ρ = dq/dV or q/V

Force and Electric field due to continuous charge distribution:-

• Due to linear charge distribution-

• Due to surface charge distribution-

• Due to volume charge distribution-

Question to find electric field due to continuous charge distribution-

1) Find electric field at point p due to linear charge distribution having linear charge density λ.

2) Electric field due to semi- circular ring.

3) Find electric field on the axis of a uniformly charged circular ring.

At centre of ring , x=0 hence net E = 0

Area vector

Yes!! Area is a vector quantity 😉

An area element dS is represented by the vector dS, such that the arrow representing the area vector ds is perpendicular to the area element. ncap is a unit vector along normal to the area element dS, then

dS = dS ncap

For 2- D surfaces - Take direction perpendicular to the surface either upwards or downwards

But

For 3- D surface - we take area vector only outward normal to the surface.

Electric flux ( phi)

• The no. of electric field lines passing normally or perpendicularly through an area.

It is scalar quantity and is denoted by phi.

Phi = E • A = E A cos theta

Where theta is an angle between E and A

SI unit is N m²/ C .

Formula - E. A is valid only if E is uniform.

When E is not uniform:

We use d phi = E . dA

The electric flux through the whole surface S can be found by integrating the above over whole surface S. Hence, total electric flux through the surface S is given by,

Phi = surface integral E . dS

• Electric flux linked with the surface in an electric field may be defined as the surface integral of the electric field over that surface.

Gauss’s Theorem:-

Gauss’s theorem states that “the total electric flux through a closed surface or 3-D surface enclosing a charge is equal to 1/ ε0 times the magnitude of the charge enclosed.”

ε0 is the absolute permittivity of free space.

If a closed surface S encloses an electric charge Q then according to Gauss’s theorem , the total electric flux through the close surface is given by,

Phi = Q/ ε0

By definition, the total electric flux through the closed surface S is given by,

where E is the electric field at that area element dS.

Therefore, Gauss’s theorem maybe expressed as,

hence Gauss’s theorem may also be stated as,

“If a closed surface encloses a charge, then surface integral of the electric field over the closed surface is equal to 1/ε0 times the charge enclosed.

Example-

• What if we consider the radius as 2R. Will the result be same as Q/ ε0 ???? Give a try

• Flux does not depend on size and shape of the closed surface.

Some important points regarding Gauss’s Law-

1) Gauss’s law is true for any closed surface no matter what its shape or size is.

2) The term Q on the right side of Gauss’s law includes the sum of all the charges enclosed by the surface , the charge may be located anywhere inside the surface.

3) If we choose a Gaussain surface such that some charges are inside and some charges are outside the surface, so the net electric field on the left of equation is due to all the charges both inside and outside the surface but the term Q on the right side of Gauss’s law represent only the total charge that is present inside the surface.

4) Surface that we choose for the application of Gauss’s law is called the Gaussian surface.

5) The Gaussian surface should not pass through any discrete charge because electric field due to a system of discrete charge is not well defined at the location of any charge.

6) The Gaussian surface can pass through a continuous charge distribution as we can approximate charge( using charge density )present inside the surface.

7) For easier calculations of electric field using Gauss’s law we choose symmetric Gaussian surface.

8) Gauss law is based on the inverse square dependence on distance. Any violation of Gauss’s law indicate departure from inverse square law.

Applications of Gauss’s law:-

1) Field due to uniformly charged infinite long wire :-